free range statistics
I write about applications of data and analytical techniques like statistical modelling and simulation to real-world situations. I show how to access and use data, and provide examples of analytical products and the code that produced them.
Recent posts
New Caledonia's nickel exports
01 January 2026
Accessing data and drawing charts for nickel exports from New Caledonia, and world nickel prices, from 2008 to 2025.
Net migration in Pacific island countries
04 December 2025
Accessing data and drawing visualisations of net migration for Pacific island countries and territories.
Visual summaries of population in Pacific islands
30 November 2025
Accessing population data for the Pacific and drawing two visual summaries of its recent and projected growth and absolute size, as used recently in a side event before the Pacific Heads of Planning and Statistics meeting in Wellington.
Distribution of p-values under the null hypothesis for discrete data
09 November 2025
p-values under the null hypothesis do not necessarily have a uniform distribution.
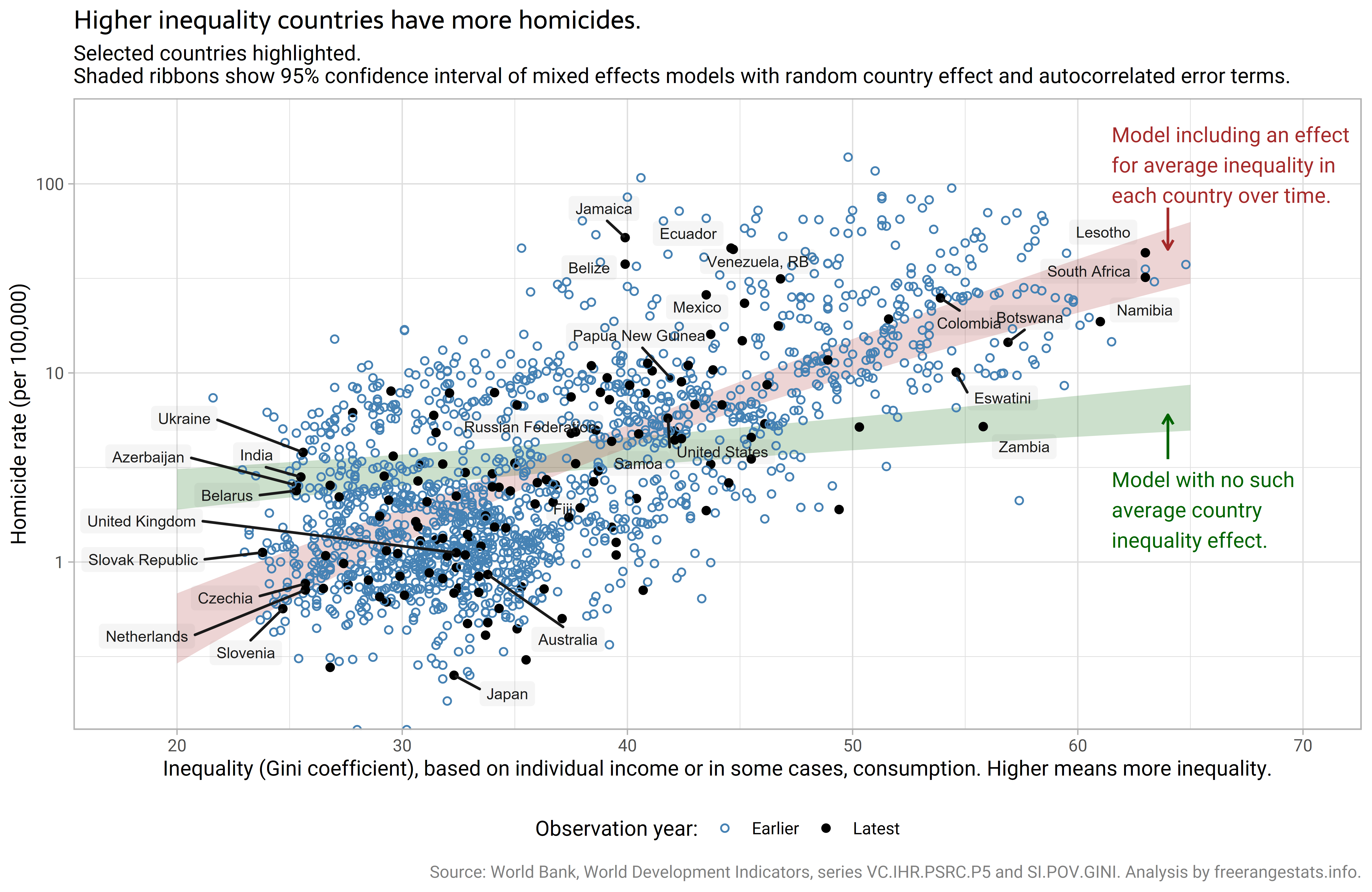
Inequality and homicide, within-country and between country
18 October 2025
Countries with higher income or consumption inequality tend to have more homicides per population. But looking at the relationship within each country's data, there does not seem to be a consistent relationship between inequality and homicide rates (that is, when there is a relationship in some countries, on average there is no evidence of such a relationship). This is an interesting multilevel or mixed-effects modelling problem that could easily trip one up.
Mapping locations related to the Amelia Earhart disappearance
05 October 2025
I draw a map of the Pacific showing the key locations associated with the disappearance of Amelia Earhart and Fred Noonan in 1937.
Ten year anniversary of Free Range Statistics
24 September 2025
A reflection on ten years, 225 posts and 350,000 words of the Free Range Statistics blog. Blogging works for me because it meets my own needs in the first instance, particularly by motivating learning and giving me a structured platform to engage with things I find interesting.
Some Papua New Guinea data doodles
07 September 2025
Motivated by an excellent recent book, I explore Papua New Guinea's statistics for GDP, population, employment and vaccination rates.
Men's domestic chores and fertility rates - Part II, technical notes
23 August 2025
A few specific notes on technical issues relating to a previous post. On drawing network graphs with different coloured edges; modelling strategy; different specifications of models; and accessing UN SDG and gender inequality data.
Men's domestic chores and fertility rates - Part I
15 August 2025
The time that men spend on domestic chores is positively related to total fertility rate. But only if you are looking at countries selected because they are rich. Overall, it's negatively related. And if you model it with both GDP per capita and gender inequality (generally, more country-level gender inequality means more children), the effect goes away altogether. At the country level, it's a statistical artefact. To look into this properly, you need individual and household-level data.