Individual-level estimates from survey data
I was motivated by web apps like the British Office of National Statistics’ How well do you know your area? and How well does your job pay? to see if I could turn the New Zealand Income Survey into an individual-oriented estimate of income given age group, qualification, occupation, ethnicity, region and hours worked. My tentative go at this is embedded below, and there’s also a full screen version available.
The job’s a tricky one because the survey data available doesn’t go to anywhere near that level of granularity. It could be done with census data of course, but any such effort to publish would come up against confidentiality problems - there are just too few people in any particular combination of category to release real data there. So some kind of modelling is required that can smooth over the actual data but still give a plausible and realistic estimate.
I also wanted to emphasise the distribution of income, not just a single measure like mean or median - something I think that we statisticians should do much more than we do, with all sorts of variables. And in particular I wanted to find a good way of dealing with the significant number of people in many categories (particularly but not only “no occupation”) who have zero income; and also the people who have negative income in any given week.
My data source is the New Zealand Income Survey 2011 simulated record file published by Statistics New Zealand. An earlier post by me describes how I accessed this, normalised it and put it into a database. I’ve also written several posts about dealing with the tricky distribution of individual incomes, listed here under the “NZIS2011” heading.
This is a longer post than usual, with a digression into the use of Random Forests (tm) to predict continuous variables, an attempt at producing a more polished plot of a regression tree than usually available, and some reflections on strengths and weakness of several different approaches to estimating distributions.
Data import and shape
I begin by setting up the environment and importing the data I’d placed in the data base in that earlier post. There’s a big chunk of R packages needed for all the things I’m doing here. I also re-create some helper functions for transforming skewed continuous variables that include zero and negative values, which I first created in another post back in September 2015.
#------------------setup------------------------
library(showtext)
library(RMySQL)
library(ggplot2)
library(scales)
library(MASS) # for stepAIC. Needs to be before dplyr to avoid "select" namespace clash
library(dplyr)
library(tidyr)
library(stringr)
library(gridExtra)
library(GGally)
library(rpart)
library(rpart.plot) # for prp()
library(caret) # for train()
library(partykit) # for plot(as.party())
library(randomForest)
# library(doMC) # for multicore processing with caret, on Linux only
library(h2o)
library(xgboost)
library(Matrix)
library(data.table)
library(survey) # for rake()
font.add.google("Poppins", "myfont")
showtext.auto()
theme_set(theme_light(base_family = "myfont"))
PlayPen <- dbConnect(RMySQL::MySQL(), username = "analyst", dbname = "nzis11")
#------------------transformation functions------------
# helper functions for transformations of skewed data that crosses zero. See
# http://ellisp.github.io/blog/2015/09/07/transforming-breaks-in-a-scale/
.mod_transform <- function(y, lambda){
if(lambda != 0){
yt <- sign(y) * (((abs(y) + 1) ^ lambda - 1) / lambda)
} else {
yt = sign(y) * (log(abs(y) + 1))
}
return(yt)
}
.mod_inverse <- function(yt, lambda){
if(lambda != 0){
y <- ((abs(yt) * lambda + 1) ^ (1 / lambda) - 1) * sign(yt)
} else {
y <- (exp(abs(yt)) - 1) * sign(yt)
}
return(y)
}
# parameter for reshaping - equivalent to sqrt:
lambda <- 0.5Importing the data is a straightforward SQL query, with some reshaping required because survey respondents were allowed to specify either one or two ethnicities. This means I need an indicator column for each individual ethnicity if I’m going to include ethnicity in any meaningful way (for example, an “Asian” column with “Yes” or “No” for each survey respondent). Wickham’s dplyr and tidyr packages handle this sort of thing easily.
#---------------------------download and transform data--------------------------
# This query will include double counting of people with multiple ethnicities
sql <-
"SELECT sex, agegrp, occupation, qualification, region, hours, income,
a.survey_id, ethnicity FROM
f_mainheader a JOIN
d_sex b on a.sex_id = b.sex_id JOIN
d_agegrp c on a.agegrp_id = c.agegrp_id JOIN
d_occupation e on a.occupation_id = e.occupation_id JOIN
d_qualification f on a.qualification_id = f.qualification_id JOIN
d_region g on a.region_id = g.region_id JOIN
f_ethnicity h on h.survey_id = a.survey_id JOIN
d_ethnicity i on h.ethnicity_id = i.ethnicity_id
ORDER BY a.survey_id, ethnicity"
orig <- dbGetQuery(PlayPen, sql)
dbDisconnect(PlayPen)
# ...so we spread into wider format with one column per ethnicity
nzis <- orig %>%
mutate(ind = TRUE) %>%
spread(ethnicity, ind, fill = FALSE) %>%
select(-survey_id) %>%
mutate(income = .mod_transform(income, lambda = lambda))
for(col in unique(orig$ethnicity)){
nzis[ , col] <- factor(ifelse(nzis[ , col], "Yes", "No"))
}
# in fact, we want all characters to be factors
for(i in 1:ncol(nzis)){
if(class(nzis[ , i]) == "character"){
nzis[ , i] <- factor(nzis[ , i])
}
}
names(nzis)[11:14] <- c("MELAA", "Other", "Pacific", "Residual")After reshaping ethnicity and transforming the income data into something a little less skewed (so measures of prediction accuracy like root mean square error are not going to be dominated by the high values), I split my data into training and test sets, with 80 percent of the sample in the training set.
set.seed(234)
nzis$use <- ifelse(runif(nrow(nzis)) > 0.8, "Test", "Train")
trainData <- nzis %>% filter(use == "Train") %>% select(-use)
trainY <- trainData$income
testData <- nzis %>% filter(use == "Test") %>% select(-use)
testY <- testData$incomeModelling income
The first job is to get a model that can estimate income for any arbitrary combination of the explanatory variables hourse worked, occupation, qualification, age group, ethnicity x 7 and region. I worked through five or six different ways of doing this before eventually settling on Random Forests which had the right combination of convenience and accuracy.
Regression tree
My first crude baseline is a single regression tree. I didn’t seriously expect this to work particularly well, but treated it as an interim measure before moving to a random forest. I use the train() function from the caret package to determine the best value for the complexity parameter cp - the minimum improvement in overall R-squared needed before a split is made. The best single tree is shown below.
One nice feature of regression trees - so long as they aren’t too large to see all at once - is usually their easy interpretability. Unfortunately this goes a bit by the wayside because I’m using a transformed version of income, and the tree is returning the mean of that transformed version. When I reverse the transform back into dollars I get a dollar number that is in effect the squared mean of the square root of the original income in a particular category; which happens to generally be close to the median, hence the somewhat obscure footnote in the bottom right corner of the plot above. It’s a reasonable measure of the centre in any particular group, but not one I’d relish explaining to a client.
Following the tree through, we see that
- the overall centre of the data is $507 income per week
- for people who work less than 23 hours, it goes down to $241; and those who work 23 or more hours receive $994.
- of those who work few hours, if they are a community and personal service worker, labourer, no occupation, or residual category occupation their average income is $169 and all other incomes it is $477.
- of those people who work few hours and are in the low paying occupations (including no occupation), those aged 15 - 19 receive $28 per week and those in other categories $214 per week.
- and so on.
It takes a bit of effort to look at this plot and work out what is going on (and the abbreviated occupation labels don’t help sorry), but it’s possible once you’ve got the hang of it. Leftwards branches always receive less income than rightwards branches; the split is always done on only one variable at a time, and the leftwards split label is slightly higher on the page than the rightwards split label.
Trees are a nice tool for this sort of data because they can capture fairly complex interactions in a very flexible way. Where they’re weaker is in dealing with relationships between continuous variables that can be smoothly modelled by simple arithmetic - that’s when more traditional regression methods, or model-tree combinations, prove useful.
The code that fitted and plotted this tree (using the wonderful and not-used-enough prp() function that allows considerable control and polish of rpart trees) is below.
#---------------------modelling with a single tree---------------
# single tree, with factors all grouped together
set.seed(234)
# Determine the best value of cp via cross-validation
# set up parallel processing to make this faster, for this and future use of train()
# registerDoMC(cores = 3) # linux only
rpartTune <- train(income ~., data = trainData,
method = "rpart",
tuneLength = 10,
trControl = trainControl(method = "cv"))
rpartTree <- rpart(income ~ ., data = trainData,
control = rpart.control(cp = rpartTune$bestTune),
method = "anova")
node.fun1 <- function(x, labs, digits, varlen){
paste0("$", round(.mod_inverse(x$frame$yval, lambda = lambda), 0))
}
# exploratory plot only - not for dissemination:
# plot(as.party(rpartTree))
svg("../img/0026-polished-tree.svg", 12, 10)
par(fg = "blue", family = "myfont")
prp(rpartTree, varlen = 5, faclen = 7, type = 4, extra = 1,
under = TRUE, tweak = 0.9, box.col = "grey95", border.col = "grey92",
split.font = 1, split.cex = 0.8, eq = ": ", facsep = " ",
branch.col = "grey85", under.col = "lightblue",
node.fun = node.fun1)
grid.text("New Zealanders' income in one week in 2011", 0.5, 0.89,
gp = gpar(fontfamily = "myfont", fontface = "bold"))
grid.text("Other factors considered: qualification, region, ethnicity.",
0.8, 0.2,
gp = gpar(fontfamily = "myfont", cex = 0.8))
grid.text("$ numbers in blue are 'average' weekly income:\nsquared(mean(sign(sqrt(abs(x)))))\nwhich is a little less than the median.",
0.8, 0.1,
gp = gpar(fontfamily = "myfont", cex = 0.8, col = "blue"))
dev.off()(Note - in working on this post I was using at different times several different machines, including some of it on a Linux server which is much easier than Windows for parallel processing. I’ve commented out the Linux-only bits of code so it should all be fully portable.)
The success rates of the various modelling methods in predicting income in the test data I put aside will be shown all in one part of this post, later.
A home-made random spinney (not forest…)
Regression trees have high variance. Basically, they are unstable, and vulnerable to influential small pockets of data changing them quite radically. The solution to this problem is to generate an ensemble of different trees and take the average prediction. Two most commonly used methods are:
- “bagging” or bootstrap aggregation, which involves resampling from the data and fitting trees to the resamples
- Random Forests (trademark of Breiman and Cutler), which resamples rows from the data and also restricts the number of variables to a different subset of variables for each split.
Gradient boosting can also be seen as a variant in this class of solutions but I think takes a sufficiently different approach for me to leave it to further down the post.
Bagging is probably an appropriate method here given the relatively small number of explanatory variables, but to save space in an already grossly over-long post I’ve left it out.
Random Forests (tm) are a subset of the broader group of ensemble tree techniques known as “random decision forests”, and I set out to explore one variant of random decision forests visually (I’m a very visual person - if I can’t make a picture or movie of something happening I can’t understand it). The animation below shows an ensemble of 50 differing trees, where each tree was fitted to a set of data sample with replacement from the original data, and each tree was also restricted to just three randomly chosen variables. Note that this differs from a Random Forest, where the restriction differs for each split within a tree, rather than being a restriction for the tree as a whole.
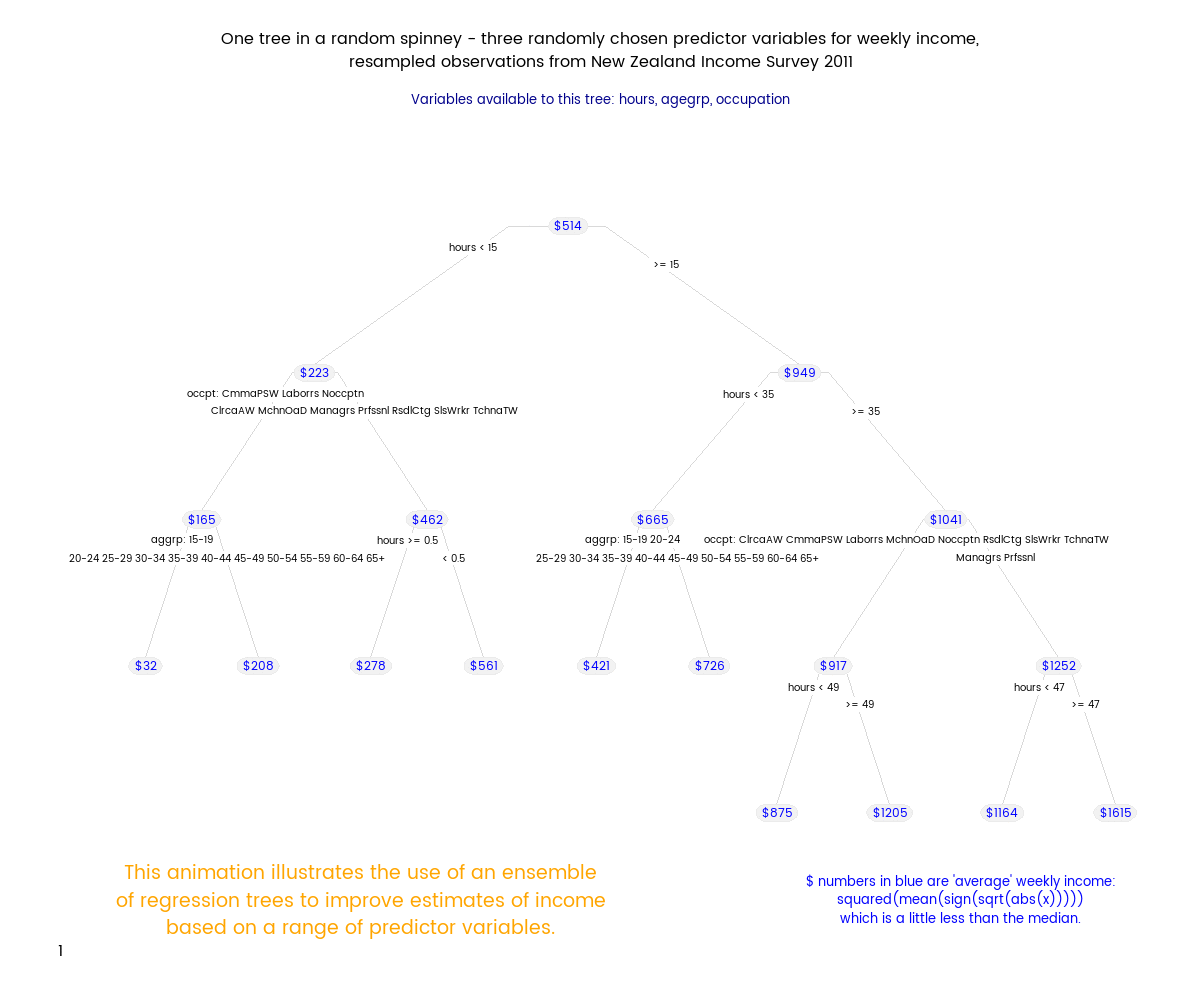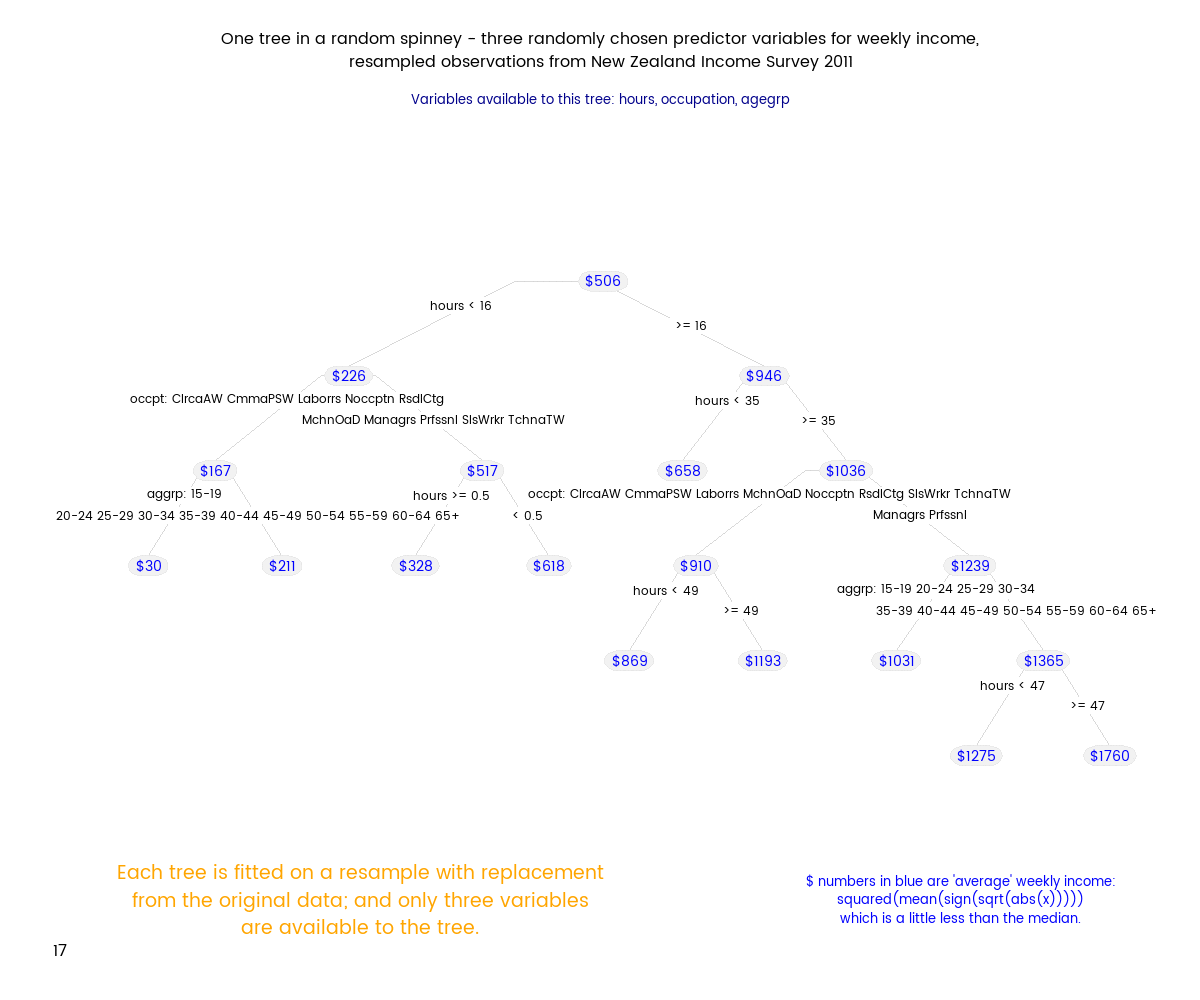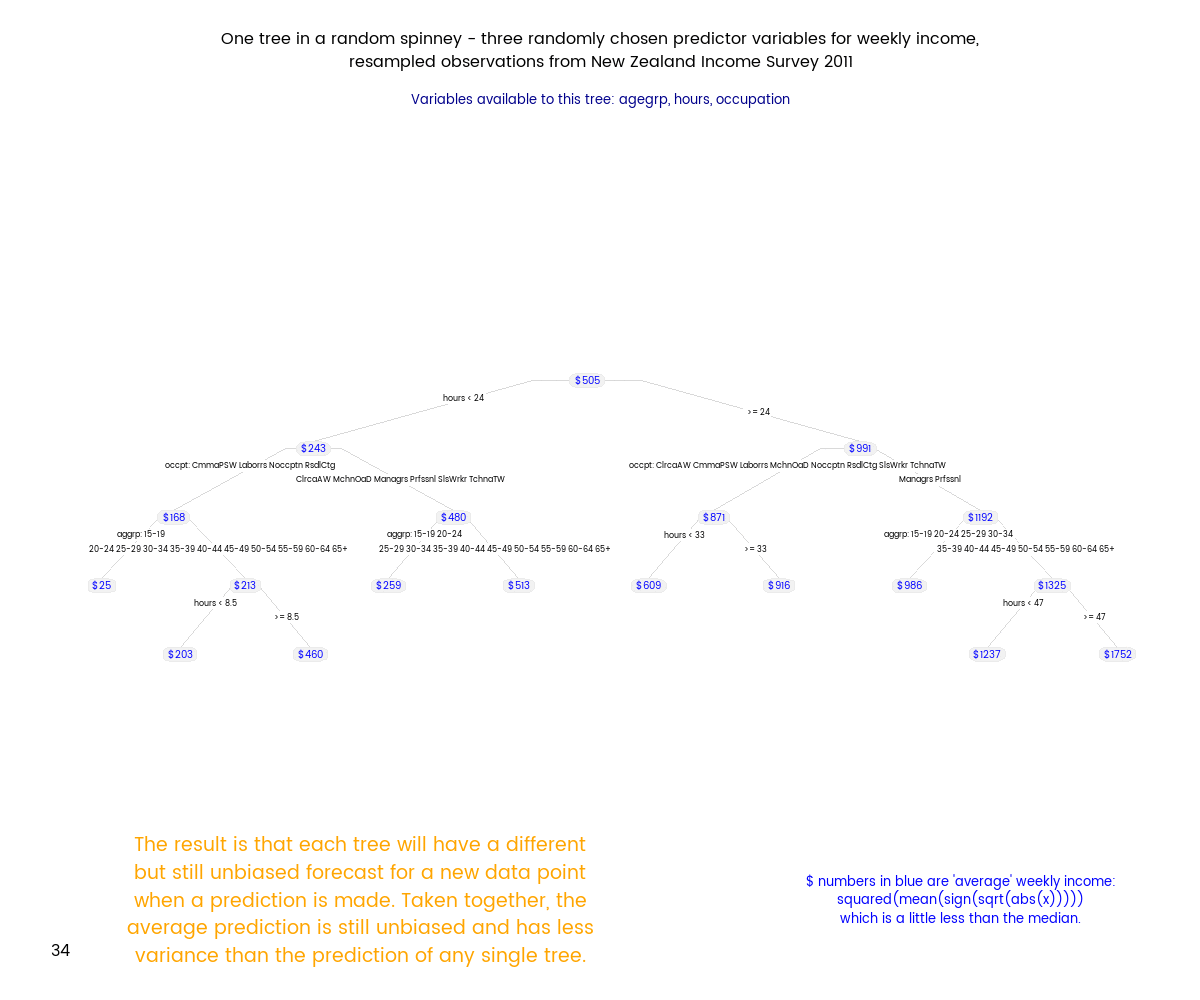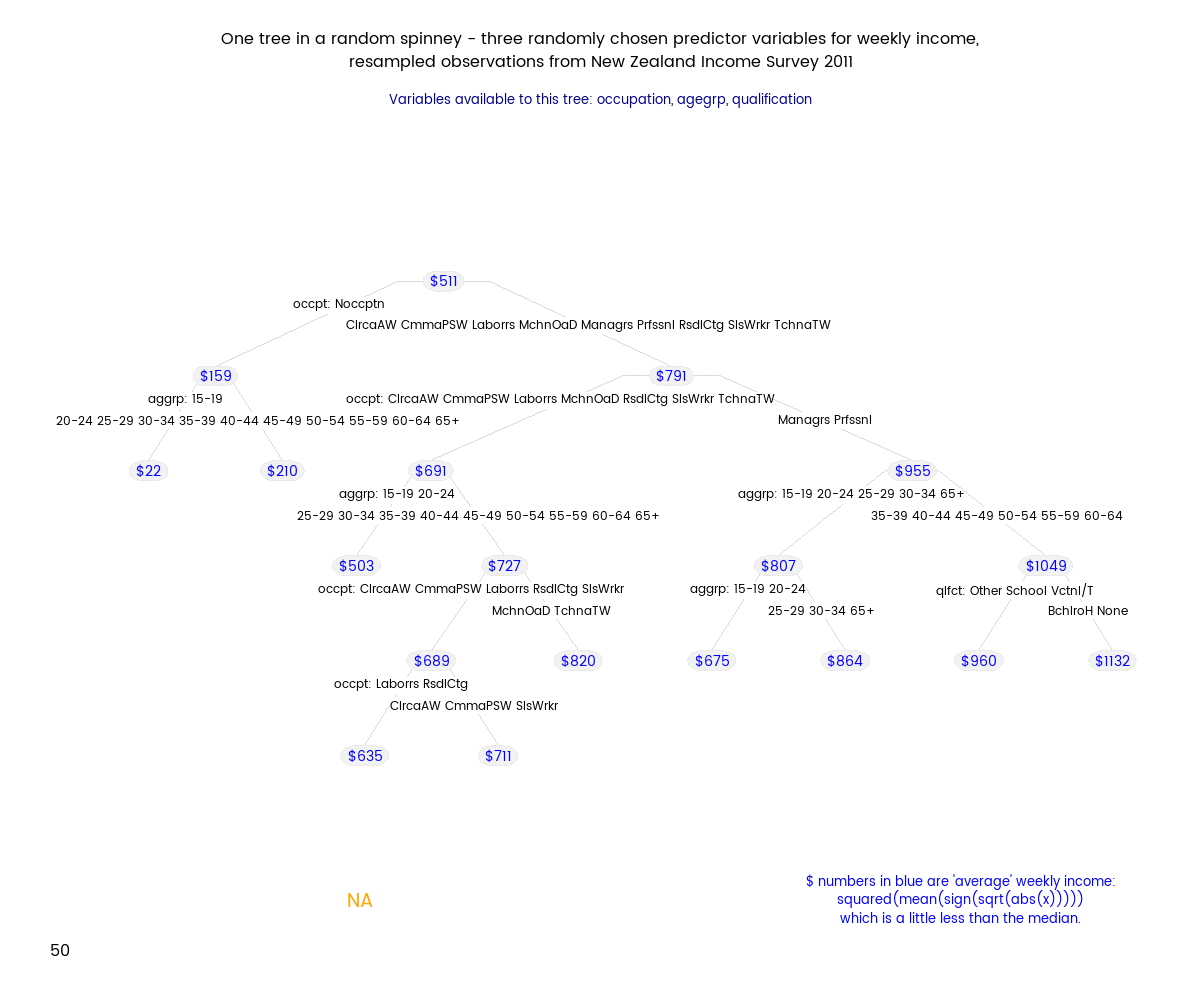
Here’s how I generated my spinney of regression trees. Some of this code depends on a particular folder structure. The basic strategy is to
- work out which variables have the most crude explanatory power
- subset the data
- subset the variables, choosing those with good explanatory power more often than the weaker ones
- use cross-validation to work out the best tuning for the complexity parameter
- fit the best tree possible with our subset of data nad variables
- draw an image, with appropriate bits of commentary and labelling added to it, and save it for later
- repeat the above 50 times, and then knit all the images into an animated GIF using ImageMagick.
#----------home made random decision forest--------------
# resample both rows and columns, as in a random decision forest,
# and draw a picture for each fitted tree. Knit these
# into an animation. Note this isn't quite the same as a random forest (tm).
# define the candidate variables
variables <- c("sex", "agegrp", "occupation", "qualification",
"region", "hours", "Maori")
# estimate the value of the individual variables, one at a time
var_weights <- data_frame(var = variables, r2 = 0)
for(i in 1:length(variables)){
tmp <- trainData[ , c("income", variables[i])]
if(variables[i] == "hours"){
tmp$hours <- sqrt(tmp$hours)
}
tmpmod <- lm(income ~ ., data = tmp)
var_weights[i, "r2"] <- summary(tmpmod)$adj.r.squared
}
svg("../img/0026-variables.svg", 8, 6)
print(
var_weights %>%
arrange(r2) %>%
mutate(var = factor(var, levels = var)) %>%
ggplot(aes(y = var, x = r2)) +
geom_point() +
labs(x = "Adjusted R-squared from one-variable regression",
y = "",
title = "Effectiveness of one variable at a time in predicting income")
)
dev.off()
n <- nrow(trainData)
home_made_rf <- list()
reps <- 50
commentary <- str_wrap(c(
"This animation illustrates the use of an ensemble of regression trees to improve estimates of income based on a range of predictor variables.",
"Each tree is fitted on a resample with replacement from the original data; and only three variables are available to the tree.",
"The result is that each tree will have a different but still unbiased forecast for a new data point when a prediction is made. Taken together, the average prediction is still unbiased and has less variance than the prediction of any single tree.",
"This method is similar but not identical to a Random Forest (tm). In a Random Forest, the choice of variables is made at each split in a tree rather than for the tree as a whole."
), 50)
set.seed(123)
for(i in 1:reps){
these_variables <- sample(var_weights$var, 3, replace = FALSE, prob = var_weights$r2)
this_data <- trainData[
sample(1:n, n, replace = TRUE),
c(these_variables, "income")
]
this_rpartTune <- train(this_data[,1:3], this_data[,4],
method = "rpart",
tuneLength = 10,
trControl = trainControl(method = "cv"))
home_made_rf[[i]] <- rpart(income ~ ., data = this_data,
control = rpart.control(cp = this_rpartTune$bestTune),
method = "anova")
png(paste0("_output/0026_random_forest/", 1000 + i, ".png"), 1200, 1000, res = 100)
par(fg = "blue", family = "myfont")
prp(home_made_rf[[i]], varlen = 5, faclen = 7, type = 4, extra = 1,
under = TRUE, tweak = 0.9, box.col = "grey95", border.col = "grey92",
split.font = 1, split.cex = 0.8, eq = ": ", facsep = " ",
branch.col = "grey85", under.col = "lightblue",
node.fun = node.fun1, mar = c(3, 1, 5, 1))
grid.text(paste0("Variables available to this tree: ",
paste(these_variables, collapse = ", "))
, 0.5, 0.90,
gp = gpar(fontfamily = "myfont", cex = 0.8, col = "darkblue"))
grid.text("One tree in a random spinney - three randomly chosen predictor variables for weekly income,
resampled observations from New Zealand Income Survey 2011", 0.5, 0.95,
gp = gpar(fontfamily = "myfont", cex = 1))
grid.text(i, 0.05, 0.05, gp = gpar(fontfamily = "myfont", cex = 1))
grid.text("$ numbers in blue are 'average' weekly income:\nsquared(mean(sign(sqrt(abs(x)))))\nwhich is a little less than the median.",
0.8, 0.1,
gp = gpar(fontfamily = "myfont", cex = 0.8, col = "blue"))
comment_i <- floor(i / 12.5) + 1
grid.text(commentary[comment_i],
0.3, 0.1,
gp = gpar(fontfamily = "myfont", cex = 1.2, col = "orange"))
dev.off()
}
# knit into an actual animation
old_dir <- setwd("_output/0026_random_forest")
# combine images into an animated GIF
system('"C:\\Program Files\\ImageMagick-6.9.1-Q16\\convert" -loop 0 -delay 400 *.png "rf.gif"') # Windows
# system('convert -loop 0 -delay 400 *.png "rf.gif"') # linux
# move the asset over to where needed for the blog
file.copy("rf.gif", "../../../img/0026-rf.gif", overwrite = TRUE)
setwd(old_dir)Random Forest
Next model to try is a genuine Random Forest (tm). As mentioned above, a Random Forest is an ensemble of regression trees, where each tree is a resample with replacement (variations are possible) of the original data, and each split in the tree is only allowed to choose from a subset of the variables available. To do this I used the {randomForests} R package, but it’s not efficiently written and is really pushing its limits with data of this size on modest hardware like mine. For classification problems the amazing open source H2O (written in Java but binding nicely with R) gives super-efficient and scalable implementations of Random Forests and of deep learning neural networks, but it doesn’t work with a continuous response variable.
Training a Random Forest requires you to specify how many explanatory variables to make available for each individual tree, and the best way to decide this is vai cross validation.
Cross-validation is all about splitting the data into a number of different training and testing sets, to get around the problem of using a single hold-out test set for multiple purposes. It’s better to give each bit of the data a turn as the hold-out test set. In the tuning exercise below, I divide the data into ten so I can try different values of the mtry parameter in my randomForest fitting and see the average Root Mean Square Error for the ten fits for each value of mtry. mtry defines the number of variables the tree building algorithm has available to it at each split of the tree. For forests with a continuous response variable like mine, the default value is the number of variables divided by three and I have 10 variables, so I try a range of options from 2 to 6 as the subset of variables for the tree to choose from at each split. It turns out the conventional default value of mtry = 3 is in fact the best:
Here’s the code for this home-made cross-validation of randomForest:
#-----------------random forest----------
# Hold ntree constant and try different values of mtry
# values of m to try for mtry for cross-validation tuning
m <- c(1, 2, 3, 4, 5, 6)
folds <- 10
cvData <- trainData %>%
mutate(group = sample(1:folds, nrow(trainData), replace = TRUE))
results <- matrix(numeric(length(m) * folds), ncol = folds)
# Cross validation, done by hand with single processing - not very efficient or fast:
for(i in 1:length(m)){
message(i)
for(j in 1:folds){
cv_train <- cvData %>% filter(group != j) %>% select(-group)
cv_test <- cvData %>% filter(group == j) %>% select(-group)
tmp <- randomForest(income ~ ., data = cv_train, ntree = 100, mtry = m[i],
nodesize = 10, importance = FALSE, replace = FALSE)
tmp_p <- predict(tmp, newdata = cv_test)
results[i, j] <- RMSE(tmp_p, cv_test$income)
print(paste("mtry", m[i], j, round(results[i, j], 2), sep = " : "))
}
}
results_df <- as.data.frame(results)
results_df$mtry <- m
svg("../img/0026-rf-cv.svg", 6, 4)
print(
results_df %>%
gather(trial, RMSE, -mtry) %>%
ggplot() +
aes(x = mtry, y = RMSE) +
geom_point() +
geom_smooth(se = FALSE) +
ggtitle(paste0(folds, "-fold cross-validation for random forest;\ndiffering values of mtry"))
)
dev.off() Having determined a value for mtry of three variables to use for each tree in the forest, we re-fit the Random Forest with the full training dataset. It’s interesting to see the “importance” of the different variables - which ones make the most contribution to the most trees in the forest. This is the best way of relating as Random Forest to a theoretical question; otherwise their black box nature makes them harder to interpret than a more traditional regression with its t tests and confidence intervals for each explanatory variable’s explanation.
It’s also good to note that after the first 300 or so trees, increasing the size of the forest seems to have little impact.
Here’s the code that fits this forest to the training data and draws those plots:
# refit model with full training data set
rf <- randomForest(income ~ .,
data = trainData,
ntrees = 500,
mtries = 3,
importance = TRUE,
replace = FALSE)
# importances
ir <- as.data.frame(importance(rf))
ir$variable <- row.names(ir)
p1 <- ir %>%
arrange(IncNodePurity) %>%
mutate(variable = factor(variable, levels = variable)) %>%
ggplot(aes(x = IncNodePurity, y = variable)) +
geom_point() +
labs(x = "Importance of contribution to\nestimating income",
title = "Variables in the random forest")
# changing RMSE as more trees added
tmp <- data_frame(ntrees = 1:500, RMSE = sqrt(rf$mse))
p2 <- ggplot(tmp, aes(x = ntrees, y = RMSE)) +
geom_line() +
labs(x = "Number of trees", y = "Root mean square error",
title = "Improvement in prediction\nwith increasing number of trees")
grid.arrange(p1, p2, ncol = 2) Extreme gradient boosting
I wanted to check out extreme gradient boosting as an alternative prediction method. Like Random Forests, this method is based on a forest of many regression trees, but in the case of boosting each tree is relatively shallow (not many layers of branch divisions), and the trees are not independent of eachother. Instead, successive trees are built specifically to explain the observations poorly explained by previous trees - this is done by giving extra weight to outliers from the prediction to date.
Boosting is prone to over-fitting and if you let it run long enough it will memorize the entire training set (and be useless for new data), so it’s important to use cross-validation to work out how many iterations are worth using and at what point is not picking up general patterns but just the idiosyncracies of the training sample data. The excellent xgboost R package by Tianqui Chen, Tong He and Michael Benesty applies gradient boosting algorithms super-efficiently and comes with built in cross-validation functionality. In this case it becomes clear that 15 or 16 rounds is the maximum boosting before overfitting takes place, so my final boosting model is fit to the full training data set with that number of rounds.
#-------xgboost------------
sparse_matrix <- sparse.model.matrix(income ~ . -1, data = trainData)
# boosting with different levels of rounds. After 16 rounds it starts to overfit:
xgb.cv(data = sparse_matrix, label = trainY, nrounds = 25, objective = "reg:linear", nfold = 5)
mod_xg <- xgboost(sparse_matrix, label = trainY, nrounds = 16, objective = "reg:linear")Two stage Random Forests
My final serious candidate for a predictive model is a two stage Random Forest. One of my problems with this data is the big spike at $0 income per week, and this suggests a possible way of modelling it does so in two steps:
- first, fit a classification model to predict the probability of an individual, based on their characteristics, having any income at all
- fit a regression model, conditional on them getting any income and trained only on those observations with non-zero income, to predict the size of their income (which may be positive or negative).
The individual models could be chosen from many options but I’ve opted for Random Forests in both cases. Because the first stage is a classification problem, I can use the more efficient H2O platform to fit it - much faster.
#---------------------two stage approach-----------
# this is the only method that preserves the bimodal structure of the response
# Initiate an H2O instance that uses 4 processors and up to 2GB of RAM
h2o.init(nthreads = 4, max_mem_size = "2G")
var_names <- names(trainData)[!names(trainData) == "income"]
trainData2 <- trainData %>%
mutate(income = factor(income != 0)) %>%
as.h2o()
mod1 <- h2o.randomForest(x = var_names, y = "income",
training_frame = trainData2,
ntrees = 1000)
trainData3 <- trainData %>% filter(income != 0)
mod2 <- randomForest(income ~ .,
data = trainData3,
ntree = 250,
mtry = 3,
nodesize = 10,
importance = FALSE,
replace = FALSE)Traditional regression methods
As a baseline, I also fit three more traditional linear regression models:
- one with all variables
- one with all variables and many of the obvious two way interactions
- a stepwise selection model.
I’m not a big fan of stepwise selection for all sorts of reasons but if done carefully, and you refrain from interpreting the final model as though it was specified in advance (which virtually everyone gets wrong) they have their place. It’s certainly a worthwhile comparison point as stepwise selection still prevails in many fields despite development in recent decades of much better methods of model building.
Here’s the code that fit those ones:
#------------baseline linear models for reference-----------
lin_basic <- lm(income ~ sex + agegrp + occupation + qualification + region +
sqrt(hours) + Asian + European + Maori + MELAA + Other + Pacific + Residual,
data = trainData) # first order only
lin_full <- lm(income ~ (sex + agegrp + occupation + qualification + region +
sqrt(hours) + Asian + European + Maori + MELAA + Other + Pacific + Residual) ^ 2,
data = trainData) # second order interactions and polynomials
lin_fullish <- lm(income ~ (sex + Maori) * (agegrp + occupation + qualification + region +
sqrt(hours)) + Asian + European + MELAA +
Other + Pacific + Residual,
data = trainData) # selected interactions only
lin_step <- stepAIC(lin_fullish, k = log(nrow(trainData))) # bigger penalisation for parameters given large datasetResults - predictive power
I used root mean square error of the predictions of (transformed) income in the hold-out test set - which had not been touched so far in the model-fitting - to get an assessment of how well the various methods perform. The results are shown in the plot below. Extreme gradient boosting and my two stage Random Forest approaches are neck and neck, followed by the single tree and the random decision forest, with the traditional linear regressions making up the “also rans”.
I was surprised to see that a humble single regression tree out-performed my home made random decision forest, but concluded that this is probably something to do with the relatively small number of explanatory variables to choose from, and the high performance of “hours worked” and “occupation” in predicting income. A forest (or spinney…) that excludes those variables from whole trees at a time will be dragged down by trees with very little predictive power. In contrast, Random Forests choose from a random subset of variables at each split, so excluding hours from the choice in one split doesn’t deny it to future splits in the tree, and the tree as a whole still makes a good contribution.
It’s useful to compare at a glance the individual-level predictions of all these different models on some of the hold-out set, and I do this in the scatterplot matrix below. The predictions from different models are highly correlated with eachother (correlation of well over 0.9 in all cases), and less strongly correlated with the actual income. This difference is caused by the fact that the observed income includes individual level random variance, whereas all the models are predicting some kind of centre value for income given the various demographic values. This is something I come back to in the next stage, when I want to predict a full distribution.
Here’s the code that produces the predicted values of all the models on the test set and produces those summary plots:
#---------------compare predictions on test set--------------------
# prediction from tree
tree_preds <- predict(rpartTree, newdata = testData)
# prediction from the random decision forest
rdf_preds <- rep(NA, nrow(testData))
for(i in 1:reps){
tmp <- predict(home_made_rf[[i]], newdata = testData)
rdf_preds <- cbind(rdf_preds, tmp)
}
rdf_preds <- apply(rdf_preds, 1, mean, na.rm= TRUE)
# prediction from random forest
rf_preds <- as.vector(predict(rf, newdata = testData))
# prediction from linear models
lin_basic_preds <- predict(lin_basic, newdata = testData)
lin_full_preds <- predict(lin_full, newdata = testData)
lin_step_preds <- predict(lin_step, newdata = testData)
# prediction from extreme gradient boosting
xgboost_pred <- predict(mod_xg, newdata = sparse.model.matrix(income ~ . -1, data = testData))
# prediction from two stage approach
prob_inc <- predict(mod1, newdata = as.h2o(select(testData, -income)), type = "response")[ , "TRUE"]
pred_inc <- predict(mod2, newdata = testData)
pred_comb <- as.vector(prob_inc > 0.5) * pred_inc
h2o.shutdown(prompt = F)
rmse <- rbind(
c("BasicLinear", RMSE(lin_basic_preds, obs = testY)), # 21.31
c("FullLinear", RMSE(lin_full_preds, obs = testY)), # 21.30
c("StepLinear", RMSE(lin_step_preds, obs = testY)), # 21.21
c("Tree", RMSE(tree_preds, obs = testY)), # 20.96
c("RandDecForest", RMSE(rdf_preds, obs = testY)), # 21.02 - NB *worse* than the single tree!
c("randomForest", RMSE(rf_preds, obs = testY)), # 20.85
c("XGBoost", RMSE(xgboost_pred, obs = testY)), # 20.78
c("TwoStageRF", RMSE(pred_comb, obs = testY)) # 21.11
)
rmse %>%
as.data.frame(stringsAsFactors = FALSE) %>%
mutate(V2 = as.numeric(V2)) %>%
arrange(V2) %>%
mutate(V1 = factor(V1, levels = V1)) %>%
ggplot(aes(x = V2, y = V1)) +
geom_point() +
labs(x = "Root Mean Square Error (smaller is better)",
y = "Model type",
title = "Predictive performance on hold-out test set of different models of individual income")
#------------comparing results at individual level------------
pred_results <- data.frame(
BasicLinear = lin_basic_preds,
FullLinear = lin_full_preds,
StepLinear = lin_step_preds,
Tree = tree_preds,
RandDecForest = rdf_preds,
randomForest = rf_preds,
XGBoost = xgboost_pred,
TwoStageRF = pred_comb,
Actual = testY
)
pred_res_small <- pred_results[sample(1:nrow(pred_results), 1000),]
ggpairs(pred_res_small)Building the Shiny app
There’s a few small preparatory steps now before I can put the results of my model into an interactive web app, which will be built with Shiny.
I opt for the two stage Random Forest model as the best way of re-creating the income distribution. It will let me create simulated data with a spike at zero dollars of income in a way none of the other models (which focus just on averages) will do; plus it has equal best (with extreme gradient boosting) in overall predictive power.
Adding back in individual level variation
After refitting my final model to the full dataset, my first substantive problem is to recreate the full distribution, with individual level randomness, not just a predicted value at each point. On my transformed scale for income, the residuals from the models are fairly homoskedastic, so decide that the Shiny app will simulate a population at any point by sampling with replacement from the residuals of the second stage model.
I save the models, the residauals, and the various dimension variables for my Shiny app.
#----------------shiny app-------------
# dimension variables for the user interface:
d_sex <- sort(as.character(unique(nzis$sex)))
d_agegrp <- sort(as.character(unique(nzis$agegrp)))
d_occupation <- sort(as.character(unique(nzis$occupation)))
d_qualification <- sort(as.character(unique(nzis$qualification)))
d_region <- sort(as.character(unique(nzis$region)))
save(d_sex, d_agegrp, d_occupation, d_qualification, d_region,
file = "_output/0026-shiny/dimensions.rda")
# tidy up data of full dataset, combining various ethnicities into an 'other' category:
nzis_shiny <- nzis %>%
select(-use) %>%
mutate(Other = factor(ifelse(Other == "Yes" | Residual == "Yes" | MELAA == "Yes",
"Yes", "No"))) %>%
select(-MELAA, -Residual)
for(col in c("European", "Asian", "Maori", "Other", "Pacific")){
nzis_shiny[ , col] <- ifelse(nzis_shiny[ , col] == "Yes", 1, 0)
}
# Refit the models to the full dataset
# income a binomial response for first model
nzis_rf <- nzis_shiny %>% mutate(income = factor(income !=0))
mod1_shiny <- randomForest(income ~ ., data = nzis_rf,
ntree = 500, importance = FALSE, mtry = 3, nodesize = 5)
save(mod1_shiny, file = "_output/0026-shiny/mod1.rda")
nzis_nonzero <- subset(nzis_shiny, income != 0)
mod2_shiny <- randomForest(income ~ ., data = nzis_nonzero, ntree = 500, mtry = 3,
nodesize = 10, importance = FALSE, replace = FALSE)
res <- predict(mod2_shiny) - nzis_pos$income
nzis_skeleton <- nzis_shiny[0, ]
all_income <- nzis$income
save(mod2_shiny, res, nzis_skeleton, all_income, nzis_shiny,
file = "_output/0026-shiny/models.rda")Contextual information - how many people are like “that” anyway?
After my first iteration of the web app, I realised that it could be badly misleading by giving a full distribution for a non-existent combination of demographic variables. For example, Maori female managers aged 15-19 with Bachelor or Higher qualification and living in Southland (predicted to have median weekly income of $932 for what it’s worth).
I realised that for meaningful context I needed a model that estimated the number of people in New Zealand with the particular combination of demographics selected. This is something that traditional survey estimation methods don’t provide, because individuals in the sample are weighted to represent a discrete number of exactly similar people in the population; there’s no “smoothing” impact allowing you to widen inferences to similar but not-identical people.
Fortunately this problem is simpler than the income modelling problem above and I use a straightforward generalized linear model with a Poisson response to create the seeds of such a model, with smoothed estimates of the number of people for each combination of demographics. I then can use iterative proportional fitting to force the marginal totals for each explanatory variable to match the population totals that were used to weight the original New Zealand Income Survey. Explaining this probably deserves a post of its own, but no time for that now.
#---------------population--------
nzis_pop <- expand.grid(d_sex, d_agegrp, d_occupation, d_qualification, d_region,
c(1, 0), c(1, 0), c(1, 0), c(1, 0), c(1, 0))
names(nzis_pop) <- c("sex", "agegrp", "occupation", "qualification", "region",
"European", "Maori", "Asian", "Pacific", "Other")
nzis_pop$count <- 0
for(col in c("European", "Asian", "Maori", "Other", "Pacific")){
nzis_pop[ , col] <- as.numeric(nzis_pop[ , col])
}
nzis_pop <- nzis_shiny %>%
select(-hours, -income) %>%
mutate(count = 1) %>%
rbind(nzis_pop) %>%
group_by(sex, agegrp, occupation, qualification, region,
European, Maori, Asian, Pacific, Other) %>%
summarise(count = sum(count)) %>%
ungroup() %>%
mutate(Ethnicities = European + Maori + Asian + Pacific + Other) %>%
filter(Ethnicities %in% 1:2) %>%
select(-Ethnicities)
# this pushes my little 4GB of memory to its limits:
mod3 <- glm(count ~ (sex + Maori) * (agegrp + occupation + qualification) + region +
Maori:region + occupation:qualification + agegrp:occupation +
agegrp:qualification,
data = nzis_pop, family = poisson)
nzis_pop$pop <- predict(mod3, type = "response")
# total population should be (1787 + 1674) * 1000 = 3,461,000. But we also want
# the marginal totals (eg all men, or all women) to match the sum of weights
# in the NZIS (where wts = 3461000 / 29400 = 117.4). So we use the raking method
# for iterative proportional fitting of survey weights
wt <- 117.4
sex_pop <- nzis_shiny %>%
group_by(sex) %>%
summarise(freq = length(sex) * wt)
agegrp_pop <- nzis_shiny %>%
group_by(agegrp) %>%
summarise(freq = length(agegrp) * wt)
occupation_pop <- nzis_shiny %>%
group_by(occupation) %>%
summarise(freq = length(occupation) * wt)
qualification_pop <- nzis_shiny %>%
group_by(qualification) %>%
summarise(freq = length(qualification) * wt)
region_pop <- nzis_shiny %>%
group_by(region) %>%
summarise(freq = length(region) * wt)
European_pop <- nzis_shiny %>%
group_by(European) %>%
summarise(freq = length(European) * wt)
Asian_pop <- nzis_shiny %>%
group_by(Asian) %>%
summarise(freq = length(Asian) * wt)
Maori_pop <- nzis_shiny %>%
group_by(Maori) %>%
summarise(freq = length(Maori) * wt)
Pacific_pop <- nzis_shiny %>%
group_by(Pacific) %>%
summarise(freq = length(Pacific) * wt)
Other_pop <- nzis_shiny %>%
group_by(Other) %>%
summarise(freq = length(Other) * wt)
nzis_svy <- svydesign(~1, data = nzis_pop, weights = ~pop)
nzis_raked <- rake(nzis_svy,
sample = list(~sex, ~agegrp, ~occupation,
~qualification, ~region, ~European,
~Maori, ~Pacific, ~Asian, ~Other),
population = list(sex_pop, agegrp_pop, occupation_pop,
qualification_pop, region_pop, European_pop,
Maori_pop, Pacific_pop, Asian_pop, Other_pop),
control = list(maxit = 20, verbose = FALSE))
nzis_pop$pop <- weights(nzis_raked)
if(round(sum(nzis_pop$pop), -4) != 3460000){
stop("You've got the wrong population of working age New Zealanders.")
}
save(nzis_pop, file = "_output/0026-shiny/nzis_pop.rda")The final shiny app
- The full screen version of the web app
- The source code




