Something missing
In my last post I developed a new scale transformation for R using the approach and platform from the ggplot2 and scales. I implemented a method proposed in 1980 by John and Draper that does some of the job of a logarithmic transform in reducing the dominance on the page of the large values, but is also continuous through zero and works for negative numbers. Here’s the image where I demonstrated that:
Tweets about the post highlighted a problem with axis labels - no labels at the points where the bulk of the data lie. This can be fixed by setting the breaks by hand but there should be a way to automate that. This post records my efforts in this direction. In the image above, you can see the big gap between $0 and $10,000 on the vertical axis (this is showing income per week, so most people are between those two numbers!) and 0 and 50 hours worked per week on the horizontal axis.
Simulated example application
To help me address this I simulated some toy data from a realistic situation - a positive, largish log-normal distribution mixed up with an unrelated normal distribution. Real data often resemble this sort of mixture (and much more complicated of course) of several different probability distributions, and it can make some of the more traditional statistical inference techniques really suffer.
Here’s the density plot of my simulated data, presented in its original scale, with a logarithm scale, and with the new modulus transform scale. There’s usually no strict rights or wrongs in this sort of exploratory analysis, but the logarithm transform does throw away all the negative values and gives a wholy erroneous focus on the big, log-normally distributed part of the data.
library(ggplot2)
library(scales)
library(tidyr)
library(dplyr)
library(showtext)
font.add.google("Poppins", "myfont")
showtext.auto()
eg <- data.frame(x = c(exp(rnorm(100, 6, 1)), rnorm(50, -50, 60)))
p <- ggplot(eg, aes(x = x)) +
geom_density() +
geom_rug() +
theme_minimal(base_family = "myfont")
p + labs(x = "Original scale")
p + scale_x_continuous("Logarithm scale", trans = "log", label = comma)
# see previous post for definition of modulus_trans():
p + scale_x_continuous("Modulus transform scale", trans = modulus_trans(0.5), label = comma)Like in my example from last week, we can see that there are no axis labels where the bulk of the data is - between 0 and 2,000. That’s what we want to fix.
Helper functions
For inspiration, I drew on the answers to this Stack Overflow question, particularly Heather Turner’s (it’s the lowest rated answer but the best in my opinion - it just came in a year after the attention had moved on). Turner was doing a similar task to me, but with the simpler log transform. I quickly realised that I needed to define some standalone functions that do the transformation and its inverse. That’s pretty straightforward
.mod_transform <- function(y, lambda){
if(lambda != 0){
yt <- sign(y) * (((abs(y) + 1) ^ lambda - 1) / lambda)
} else {
yt = sign(y) * (log(abs(y) + 1))
}
return(yt)
}
.mod_inverse <- function(yt, lambda){
if(lambda != 0){
y <- ((abs(yt) * lambda + 1) ^ (1 / lambda) - 1) * sign(yt)
} else {
y <- (exp(abs(yt)) - 1) * sign(yt)
}
return(y)
}Approach
My strategy is going to be to
- transform the data with
.mod_transform() - use the
pretty()function from base R to determine nearly-equally spaced breaks along that transformed range - transform those breaks back to the original scale with
.mod_inverse() - tidy up the numbers by rounding them, rounding more aggressively the larger the number
The whole thing gets wrapped up in a function that can be used by the breaks = argument from a scale like scale_x_continuous. Let’s see where we’re heading:
One tricky catch was the final tidying up / rounding. At one point I made the mistake of trying to copy what pretty() does and pick the nearest number that is 1, 2 or 5 times a multiple of 10. This made the gridlines look oddly spaced; it makes sense for a logarithm transform but not for our more complex one.
So here’s how I did it. I broke it into two more functions, because I thought prettify() (which does the rounding) might be useful for something else (I’m sure there’s something that does this already in R, maybe even in base R, but it’s easier to write than to find).
prettify <- function(breaks){
# round numbers, more aggressively the larger they are
digits <- -floor(log10(abs(breaks))) + 1
digits[breaks == 0] <- 0
return(round(breaks, digits = digits))
}
mod_breaks <- function(lambda, n = 8, prettify = TRUE){
function(x){
breaks <- .mod_transform(x, lambda) %>%
pretty(n = n) %>%
.mod_inverse(lambda)
if(prettify){
breaks <- prettify(breaks)
}
return(breaks)
}
}Usage is simple. Here’s how I drew the two density plots above:
p +
scale_x_continuous(trans = modulus_trans(0.2), label = comma,
breaks = mod_breaks(lambda = 0.2, prettify = FALSE)) +
theme(panel.grid.minor = element_blank()) +
ggtitle("Regular breaks")
p +
scale_x_continuous(trans = modulus_trans(0.2), label = comma,
breaks = mod_breaks(lambda = 0.2, prettify = TRUE)) +
theme(panel.grid.minor = element_blank()) +
ggtitle("Rounded breaks")
Applying to the New Zealand Income Survey 2011
OK, now I can apply it to the real data from my previous post (and a post earlier than that shows how to get it into the database I’m using here). First, here’s the density of individual weekly income from all sources in that 2011 survey:
# connect to database
library(RODBC)
PlayPen <- odbcConnect("PlayPen_prod")
sqlQuery(PlayPen, "use nzis11")
inc <- sqlQuery(PlayPen, "select * from vw_mainheader")
ggplot(inc, aes(x = income)) +
geom_density() +
geom_rug() +
scale_x_continuous(trans = modulus_trans(0.25), label = dollar,
breaks = mod_breaks(0.25)) +
theme_minimal(base_family = "myfont")
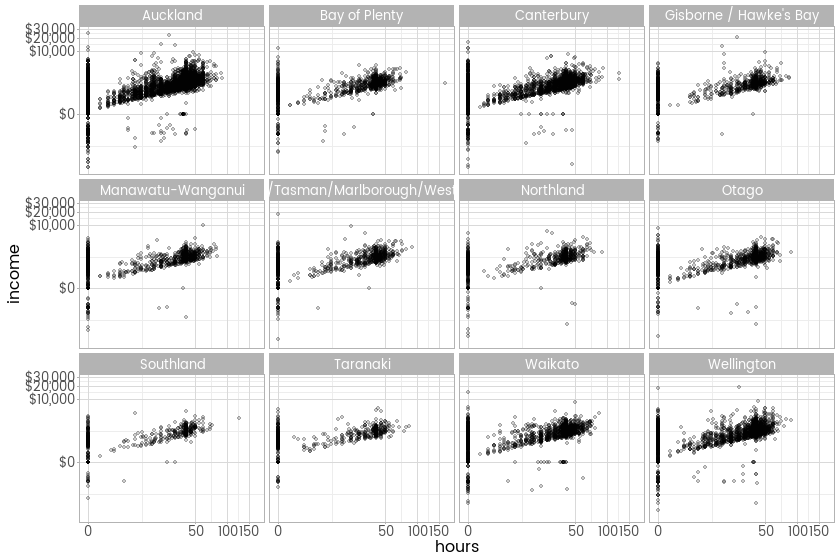
And now here’s something new (but similar to last week) - weekly income compared hours worked, by occupation:
ggplot(inc, aes(x = hours, y = income)) +
facet_wrap(~occupation, ncol =2) +
geom_point(alpha = 0.2) +
scale_x_continuous(trans = modulus_trans(0.25), breaks = mod_breaks(0.25)) +
scale_y_continuous(trans = modulus_trans(0.25), label = dollar, breaks = mod_breaks(0.25)) +
theme_light(base_family = "myfont")
Much better, particularly if I’m going to use this transformation a lot, and it looks like the right one to use for data that is mostly positive and right tailed, but has a bunch of negatives thrown in too.



